فراکتال (Fractal)
فراکتال (Fractal) یا بَرخال یا فرکتال شاخه جدیدی از ریاضیات و هنر است. اغلب مردم فراکتالها را فقط به عنوان تصاویر زیبایی میشناسند که برای پسزمینه صفحه نمایش رایانه یا کارت پستال به کار میبرند. اما فراکتالها واقعاً چه هستند؟ در این آموزش با فراکتالها آشنا میشویم.
مقدمه
اغلب سیستمهای فیزیکی در طبیعت و بسیاری از مصنوعات بشر اَشکال هندسی منظمی مطابق هندسه استاندارد اقلیدسی ندارند. هندسه فراکتالی روشهای تقریباً نامحدودی برای توصیف، سنجش و پیشبینی این پدیدههای طبیعی ارائه میکند. اما آیا میتوان با استفاده از معادلات ریاضی کل جهان را تعریف کرد؟ در ادامه، درباره چهار فراکتال مشهور بحث میکنیم و مهمترین ویژگیهای فراکتال را توضیح میدهیم که موجب شدهاند برای حوزههای مختلف علمی مفید باشند.
بسیاری از افراد مجذوب تصاویری هستند که به آنها فراکتال میگویند. هندسه فراکتالی فراتر از تصور معمول مردم درباره ریاضیات است که آن را فرمولهای پیچیده و کسلکننده میبینند. این هندسه، ریاضیات را با هنر در میآمیزد و نشان میدهد که معادلهها چیزی جز یک مجموعه عدد نیستند. آنچه فراکتالها را جذابتر میکند، این است که بهترین توصیفهای ریاضیاتی موجود برای بسیاری از پدیدههای طبیعی، مانند سواحل، کوهها یا بخشهایی از موجودات زنده هستند.
اگرچه هندسه فراکتالی ارتباط نزدیکی با فناوری و رایانه دارد، اما برخی افراد مدتها قبل از اختراع رایانه بر روی فراکتال کار کرده بودند. این افراد نقشهبرداران بریتانیایی بودند که در اندازهگیری طول ساحل انگلیس با مشکل روبهرو شدند. خط ساحلی که روی یک نقشه در مقیاس بزرگ به دست آمده بود، تقریباً نیمی از طول خط ساحلی بود که در یک نقشه دقیق و با جزئیات اندازهگیری شده بود. هرچه این دو نقشه به یکدیگر نزدیکتر میشدند، خط ساحلی دقیقتر و طولانیتر میشد. آنها به این نکته پی نبرده بودند که یکی از اصلیترین ویژگیهای فراکتالها را کشف کردهاند.
ویژگیهای فراکتال
دو مورد از مهمترین خصوصیات فراکتالها، خودتشابهی (Self-similarity) و بُعد غیرصحیح (Non-integer Dimension) آنها است.
اما خودتشابهی چیست؟ اگر به برگ سرخس دقت کنید، متوجه میشوید که شکل هر برگ کوچک (بخشی از برگ بزرگتر) شبیه کل برگ سرخس است و میتوان گفت که برگ سرخس شبیه خود سرخس است. همین مورد برای فراکتالها نیز وجود دارد: میتوانید آنها را بارها و بارها بزرگنمایی کنید و بعد از هر مرحله، همان شکل را ببینید.

توضیح غیرصحیح بودن بعد فراکتال کمی دشوارتر است. هندسه کلاسیک با اشیائی با ابعاد صحیح سر و کار دارد: نقاط صفربعدی، خطوط یکبعدی، منحنیها و شکلهای صفحه دوبعدی مانند مربعها و دایرهها، و اجسام سهبعدی مانند مکعبها و کرهها. با این حال، بسیاری از پدیدههای طبیعی را میتوان با استفاده از ابعادی بین دو عدد حسابی بهتر توصیف کرد. بنابراین، در حالی که یک بعد یک خط مستقیم یک است، بسته به اینکه فضا به همان اندازه پیچ خورده و منحنی بسته شود، یک منحنی فراکتال بعدی بین یک تا دو خواهد داشت. هرچه فرکتال مسطح یک صفحه را پر کند، بعد آن به دو نزدیک میشود. به همین ترتیب، «منظره فراکتال کوهستانی» به ابعادی بین دو تا سه میرسد. بنابراین، بُعدِ یک منظره فراکتال که از یک تپه بزرگِ پوشیده از تپههای ریز و کوچک تشکیل شده است، به دو نزدیک میشود. اما اگر کوه شامل یک سطح ناهموار متشکل از تعداد زیادی تپه متوسط باشد، بعدی نزدیک به سه خواهد داشت.
فراکتالها انواع مختلفی دارند که در اینجا دو نوع از محبوبترین آنها را معرفی میکنیم: فراکتالهای عدد مختلط (Complex Number) و فراکتالهای سیستم تابع تکرارشونده (Iterated Function System) یا IFS.
فراکتالهای عدد مختلط
قبل از توصیف این نوع فراکتال، کمی درباره نظریه اعداد مختلط توضیح میدهیم.
یک عدد مختلط شامل یک عدد حقیقی است که با یک عدد موهومی جمع میشود. معمولاً وقتی یک عدد مختلط را در صفحه مختلط نشان میدهیم، آن را یک «نقطه» در نظر میگیریم. اگر عدد مختلط Z=a+b⋅i را داشته باشیم، مختصات این نقطه، a (محور افقی حقیقی) و b (محور عمودی موهومی) هستند. واحد اعداد موهومی i=√−1 است.
دو محقق برجسته در زمینه فراکتالهای عدد مختلط، «گاستون موریس ژولیا» (Gaston Maurice Julia) و «بنوآ مندلبرو» (Benoit Mandelbrot) هستند.
گاستون موریس ژولیا در اواخر قرن نوزدهم در الجزایر به دنیا آمد. او زندگی خود را صرف مطالعه تکرار چندجملهایها و توابع گویا کرد. ژولیا در حدود دهه 1920، پس از انتشار مقاله خود در مورد تکرار یک تابع گویا مشهور شد. با این حال، او را پس از مرگ به فراموشی سپردند.
در دهه 1970، کار گاستون موریس ژولیا توسط بنوآ مندلبرو لهستانی احیا شد و محبوبیت پیدا کرد. مندلبرو که کارمند شرکت آیبیام بود، با الهام از کار ژولیا و با کمک گرافیک رایانهای، توانست اولین تصاویر را از زیباترین فراکتالهایی که تاکنون شناخته شدهاند به نمایش بگذارد.
مجموعه مندلبرو
مجموعه مندلبرو (Mandelbrot Set) مجموعهای از نقاط روی یک صفحه مختلط است. برای ساخت مجموعه مندلبرو باید از یک الگوریتم مبتنی بر فرمول بازگشتی استفاده کنیم:
Zn=Z2n−1+C
نقاط روی صفحه مختلط را به دو دسته تقسیم میکنیم:
- نقاط درون مجموعه مندلبرو
- نقاط بیرون مجموعه مندلبرو
تصویر زیر، بخشی از صفحه مختلط را نشان میدهد. نقاط مجموعه مندلبرو با رنگ سیاه مشخص شدهاند.
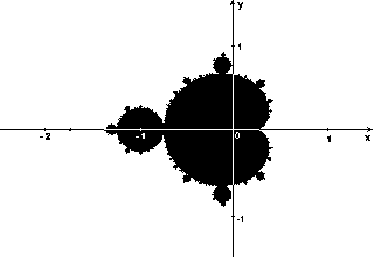 همچنین میتوان رنگی را به نقاط خارج از مجموعه مندلبرو اختصاص داد که رنگ آنها به تعداد تکرارها برای تعیین نقاط خارج از مجموعه مندلبرو بستگی دارد.
همچنین میتوان رنگی را به نقاط خارج از مجموعه مندلبرو اختصاص داد که رنگ آنها به تعداد تکرارها برای تعیین نقاط خارج از مجموعه مندلبرو بستگی دارد.
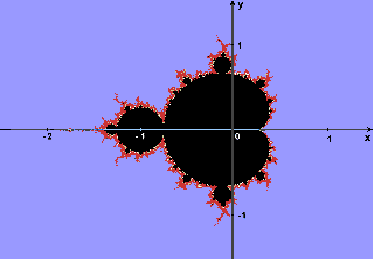
تشکیل مجموعه مندلبرو
برای تشکیل مجموعه مندلبرو باید یک نقطه (C) را روی صفحه مختلط برگزینیم. عدد مختلط متناظر با این نقطه C=a+b⋅i است.
بعد از محاسبه مقدار رابطه بازگشتی Z1=Z20+C و با قرار دادن مقدار صفر برای Z0، مقدار C به عنوان نتیجه به دست میآید. گام بعدی شامل استفاده از مقدار Z1 و تکرار محاسبات است. اکنون، نتیجه عدد مختلط C2+C است. همینگونه فرایند را تکرار و تکرار میکنیم.
این فرایند را میتوان به عنوان «کوچ» یا جابهجایی (Migration) نقطه اولیه C در صفحه نمایش داد. اگر بارها و بارها تابع را تکرار میکنیم چه اتفاقی برای نقطه خواهد افتاد؟ آیا در نزدیکی مبدأ باقی خواهد ماند یا از آن فاصله خواهد گرفت و فاصله آن از مبدأ بدون محدودیت افزایش پیدا میکند؟ در حالت اول، C متعلق به مجموعه مندلبرو است (یکی از نقاط سیاه موجود در تصویر)؛ در غیر این صورت، نقطه به بینهایت میرود و بسته به سرعتی که نقطه از مبدأ فرار میکند، رنگی به C اختصاص میدهیم.
از زاویه دیگری نیز میتوانیم به الگوریتم بنگریم. فرض میکنیم تمام نقاط موجود در صفحه توسط هر دو مجموعه بینهایت و مجموعه مندلبرو جذب شدهاند. این فرض باعث میشود درک بهتری داشته باشیم، زیرا:
- نقاط دور از مجموعه مندلبرو سریعاً به سمت بینهایت حرکت میکنند.
- نقاط نزدیک به مجموعه مندلبرو به آرامی به بینهایت فرار میکنند.
- نقاط داخل مجموعه مندلبرو هرگز به بینهایت فرار نمیکنند.
مجموعههای ژولیا
مجموعههای ژولیا (Julia sets) کاملاً با مجموعه مندلبرو در ارتباط هستند و عملکرد تکراری که برای تولید آنها به کار میرود، همان فرایند مجموعه مندلبرو است. تنها تفاوت، نحوه استفاده از این فرمول است. برای ترسیم تصویری از مجموعه مندلبرو، همیشه با شروع از Z0=0 فرمول را برای هر نقطه C در صفحه مختلط تکرار میکنیم. اگر بخواهیم از یک مجموعه ژولیا تصویری بسازیم، در کل مراحل تشکیل آن، C باید ثابت باشد، در حالی که مقدار Z0 متغیر است. مقدار C، شکل مجموعه ژولیا را تعیین میکند. به عبارت دیگر، هر نقطه از صفحه مختلط با یک مجموعه خاص ژولیا متناظر است.
تشکیل مجموعه ژولیا
باید نقطه C را از صفحه مختلط انتخاب کنیم. الگوریتم زیر، مشخص میکند که آیا یک نقطه Z در صفحه مختلط) متعلق به مجموعه ژولیا متناظر با C است یا خیر و همچنین، رنگی را که باید به آن اختصاص دهید تعیین میکند. برای اینکه ببینیم Z به مجموعه تعلق دارد، باید تابع Z1=Z20+C را با استفاده از Z0=Z تکرار کنیم. اما چه اتفاقی برای نقطه اولیه Z در هنگام تکرار فرمول رخ میدهد؟ در نزدیکی مبدأ باقی خواهد ماند یا از آن فاصله خواهد گرفت و فاصله آن از مبدأ بدون محدودیت افزایش مییابد؟ در حالت اول، نقطه متعلق به مجموعه ژولیا است. در غیر این صورت، به بینهایت میرود و بسته به سرعت فرار نقطه از مبدأ، رنگی به Z اختصاص میدهیم. برای تولید تصویری از کل مجموعه ژولیا که متناظر با C است، باید این روند را برای تمام نقاط Z تکرار کنیم که مختصات آنها در این محدوده گنجانده شده است:
−2<x<2;−1.5<y<1.5
مهمترین رابطه بین مجموعههای ژولیا و مجموعه مندلبرو این است که وقتی مجموعه مندلبرو همبند باشد (یک قطعه تکی)، یک مجموعه ژولیا همبند است اگر متناظر با یک نقطه درون مجموعه مندلبرو باشد. برای مثال، مجموعه ژولیای متناظر با C1 در شکل زیر همبند، و مجموعه ژولیای متناظر با C2 ناهمبند است.
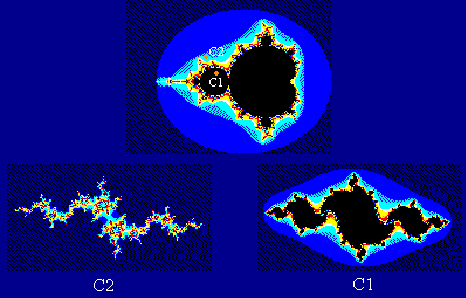
فراکتالهای سیستم تابع تکراری
فراکتالهای سیستم تابع تکراری (IFS) بر اساس تبدیلات ساده صفحه، مانند تغییر مقیاس، جابهجایی و چرخش محورها ایجاد میشوند. ایجاد یک فراکتال IFS شامل مراحل زیر است:
- تعریف مجموعهای از تبدیلات صفحه
- رسم یک الگوی اولیه در صفحه (هر الگویی)
- تبدیل الگوی اولیه با استفاده از تبدیلات تعریف شده در مرحله اول
- تبدیل تصویر جدید (ترکیبی از الگوهای اولیه و تبدیل شده) با استفاده از همان مجموعه تبدیلات
- تکرار مرحله چهارم هر چند بار ممکن (در تئوری، این روش میتواند بارها و بارها تکرار شود.)
معروفترین فرکتالهای ISF مثلث سیرپینسکی و برفدانه کخ هستند.
مثلث سیرپینسکی
مثلث سیرپینسکی (Sierpinski Triangle) فراکتالی است که با وصل کردن نقاط میانی هریک از اضلاع یک مثلث متساویالاضلاع تشکیل میشود. تکرارها را باید بارها و بارها انجام دهیم. شکلهای زیر چهار مرحله اول ساخت مثلث سیرپینسکی را نشان میدهد.
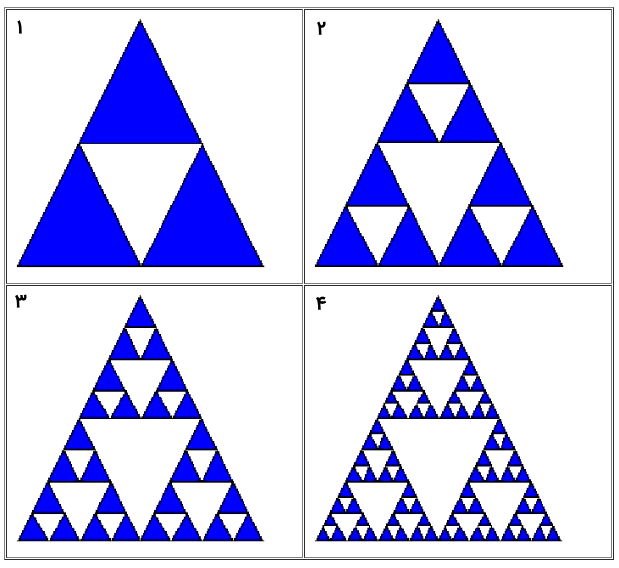
تصویر متحرک زیر نیز تکرار در تشکیل مثلث سیرپینسکی را به خوبی نشان میدهد.

با استفاده از این مثال میتوانیم اثبات کنیم بعد فراکتالها عددی صحیح نیست.
ابتدا باید دریابیم که «بعد» یک جسم با افزایش بعد خطی آن چگونه رفتار میکند. در یک بعد میتوانیم یک بخش خط را در نظر بگیریم. اگر بعد خطی قطعه خط دو برابر شود، طول (اندازه مشخصه) خط نیز دو برابر میشود. در دو بعد، اگر ابعاد خطی یک مربع مثلاً دو برابر شود، اندازه مشخصه، یعنی مساحت، با ضریب 4 افزایش مییابد. همچنین در سه بعد، اگر بعد خطی یک جعبه دو برابر شود، حجم آن با ضریب 8 افزایش مییابد.
این رابطه بین بعد D، مقیاس خطی L و نتیجه افزایش اندازه S را میتوان به صورت کلی تعمیم داد و به شکل زیر نوشت:
S=L⋅D
با بازنویسی مجدد این فرمول، بسته به نحوه تغییر اندازه به عنوان تابعی از مقیاسبندی خطی، توصیفی را برای بعد به دست میآوریم:
D=log(S)log(L)
در مثال بالا، مقدار D، بسته به ابعاد هندسی، یک عدد صحیح (۱، ۲ یا ۳) است. این رابطه برای همه اشکال اقلیدسی برقرار است. اما در مورد فراکتالها چه میتوان گفت؟
با نگاهی به تصویر اولین مرحله در ساخت مثلث سیرپینسکی، به این نکته پی میبریم که اگر بعد خطی مثلث پایه (L) دو برابر شود، مساحت کل فراکتال (مثلثهای آبی) با ضریب سه افزایش مییابد (S).
با استفاده از الگوی گفته شده در بالا، میتوان بعد مثلث سیرپینسکی را محاسبه کرد:
D=log(3)log(2)
نتیجه این محاسبات، غیرصحیح بودن بعد فراکتال را نشان میدهد.
برفدانه کخ
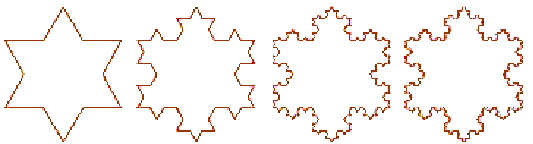
برای ساختن برفدانه کخ (Koch Snowflake)، باید از مثلث متساویالاضلاعی با طول ضلع مثلاً ۱ شروع کنیم. در میانه هر ضلع، مثلث متساویالاضلاع جدیدی با ضلع یکسوم اضافه خواهیم کرد و این روند را به تعداد نامحدود تکرار میکنیم. طول مرزها یا همان محیط بینهایت است (3⋅43⋅43⋅43⋅⋯). با این حال، مساحت کمتر از مساحت یک دایره محیطی در اطراف مثلث اصلی است. این بدان معنی است که یک خط بینهایت طولانی یک سطح محدود را احاطه کرده است. ساختار نهایی برفدانه کخ شبیه خط ساحلی است.
شکل زیر، چهار گام تشکیل برفدانه کخ را نشان میدهد.
تصویر متحرک زیر نیز تکرار در تشکیل برفدانه کخ را به خوبی نشان میدهد.
سایر فراکتالهای IFS
شکل زیر، برگ سرخس و مارپیچ را نشان میدهد که فراکتالهای IFS هستند.

کاربرد فراکتالها
هندسه فراکتالی در بسیاری از حوزههای علمی مانند اخترفیزیک و علوم زیستی کاربرد دارد و به یکی از مهمترین تکنیکها در گرافیک رایانهای تبدیل شده است.
فراکتالها در اخترفیزیک
هیچکس نمیداند که دقیقاً چند ستاره در آسمان میدرخشد، اما آیا تا به حال فکر کردهاید که این ستارهها چگونه شکل گرفتهاند و در نهایت منزلگاه خود را در جهان یافتهاند؟ اخترفیزیکدانان بر این باورند که مهمترین مسئله ماهیت فراکتالی گاز میانستارهای بوده و توزیع فراکتالها مانند مسیر دود یا ابرهای موجدار در آسمان، سلسلهمراتبی است. آشفتگی موجب تشکیل ابرها در آسمان و ابرهای موجود در فضا میشود و الگویی نامنظم اما تکراری به آنها میدهد که بدون کمک گرفتن از هندسه فراکتالی توصیف آن غیرممکن است.
فراکتالها در علوم زیستی
زیستشناسان، به طور سنتی با استفاده از نمایش اقلیدسی اشیاء یا دنبالههای طبیعی، طبیعت را مدل کردهاند. آنها ضربان قلب را به عنوان امواج سینوسی، درختان مخروطی را به عنوان مخروطها، زیستگاههای حیوانات به عنوان سطوح و غشاهای سلولی را به عنوان منحنی یا سطوح ساده نشان میدادند. با این حال، دانشمندان دریافتهاند که بسیاری از سازههای طبیعی با استفاده از هندسه فراکتالی بهتر توصیف میشوند. سیستمها و فرایندهای زیستی معمولاً با سطوح مختلفی از زیرسازهها، با همان الگوی کلی که در یک توالی رو به کاهش است تکرار میشود.
به همین ترتیب، دانشمندان دریافتند که معماری اساسی کروموزوم شبیه درخت است. هر کروموزوم از بسیاری از مینیکروموزومها تشکیل شده است؛ بنابراین میتوان آن را به عنوان فراکتال در نظر گرفت. به عنوان مثال، برای کروموزوم انسان، ابعاد فراکتالی D برابر با ۲٫۳۴ است (بین بعد صفحه و بعد فضا).
خودتشابهی نیز در توالی DNA یافت شده است. به عقیده برخی زیستشناسان، از خواص فراکتال DNA میتوان برای حل روابط تکاملی در حیوانات استفاده کرد.
شاید در آینده زیستشناسان از هندسه فراکتالی برای ایجاد مدلهای جامع الگوها و فرایندهای مشاهده شده در طبیعت نیز استفاده کنند.
فراکتالها در گرافیک رایانهای
بیشترین استفاده از فراکتالها در زندگی روزمره در علم رایانه است. بسیاری از طرحهای فشردهسازی تصویر از الگوریتمهای فراکتال برای فشردهسازی پروندههای گرافیکی رایانه به کمتر از یکچهارم از اندازه اصلی استفاده میکنند.
گرافیستها از اشکال فراکتال زیادی برای ایجاد مناظر با بافتهای ویژه و سایر مدلهای پیچیده استفاده میکنند.

همچنین، میتوان انواع تصاویر واقعی فراکتالی را از مناظر طبیعی، مانند مناظر قمری، کوهستانها و خطوط ساحلی ایجاد کرد. تصاویر فراکتالی در جلوههای ویژه بسیاری در فیلمها و همچنین در تبلیغات تلویزیونی وجود دارند. از سیگنالهای فراکتالی نیز میتوان برای مدلسازی اشیاء طبیعی استفاده کرد که به ما این امکان را میدهد تا از نظر ریاضی محیط خود را با دقت بالاتری نسبت به گذشته تعریف کنیم.

جمعبندی
بسیاری از دانشمندان دریافتهاند که هندسه فراکتالی ابزاری قدرتمند برای کشف اسرار طیف گستردهای از سیستمها و حل مسائل مهم در علوم کاربردی است و به همین دلیل، تعداد سیستمهای فیزیکی فراکتال شناخته شده به سرعت در حال رشد است.
فراکتالها دقت ما را در توصیف و طبقهبندی اشیاء تصادفی یا ارگانیک بهبود بخشیدهاند، اما شاید هنوز کامل نباشند. شاید آنها فقط به دنیای طبیعی ما نزدیکتر شدهاند و هنوز خود آن نیستند. برخی دانشمندان هنوز بر این باورند که واقعیت تصادفی بودن است و هیچ معادله ریاضی قادر نیست آن را به طور کامل توصیف کند. هرچند، نمیتوان گفت کدام گفته درست است.
شاید برای بسیاری از افراد فراکتالها هرگز چیزی بیش از تصاویری زیبا نباشند.

