سرعت نور و محاسبه آن از معادلات ماکسول
- نوشته شده توسط Super User
- دسته: آموزش
بنابر اصل دوم نسبیت خاص آلبرت اینشتین، نهایت سرعت اجسام مادی محدود بوده و نمیتوانند به سرعتی بیشتر از سرعت نور دست پیدا کنند. در این مقاله قصد داریم تا با زبانی ساده به محاسبه سرعت نور یا به طور کلی سرعت امواج الکترومغناطیسی توسط معادلات ماکسول بپردازیم. با ما در ادامه این مقاله همراه باشید.
بر اساس متون تاریخ علم، میتوان گفت اولین نفری که سرعت نور را محاسبه کرد، ستارهشناسی دانمارکی به نام اوله رومر (Ole Christensen Roemer) بود. رومر در حدود سال 1676 میلادی سرعت نور را بر اساس محاسبات نجومی خود از قمر سیاره مشتری، حدود ۱۴۰ کیلومتر در ثانیه اندازهگیری کرد. امروزه میدانیم که سرعت نور به طور تقریبی برابر با ۲۹۹٬۷۹۲٬۴۵۸ متر بر ثانیه است.

محاسبه سرعت نور
در این بخش قصد داریم تا سرعت نور را به کمک فرم دیفرانسیلی معادلات ماکسول به دست آوریم. در واقع معادله موج الکترومغناطیسی را از معادلات ماکسول به دست آورده و سپس از جواب عمومی معادله موج، سرعت نور را محاسبه میکنیم. جهت یادآوری معادلات مذکور به فرم زیر هستند:
▽.E=0
(1)
▽.B=0
(2)
▽×E= –∂B∂t
(3)
▽×B=μ0ε0∂E∂t
(4)
توجه داشته باشید که در اینجا محاسبات را در محیط خلأ (نهایت سرعت نور) انجام میدهیم. از این حیث چگالی بار ρ و چگالی جریان J را در معادلات فوق صفر فرض کردیم. دو پارامتر ضریب گذردهی الکتریکی ε و مغناطیسی μ به طور کلی خواص الکترومغناطیسی محیط را مشخص میکنند. اندیس صفر، مقدار این دو پارامتر را در خلأ که عددی ثابت است، بیان میکند.
ε0=8.854787×10−12 (C2N.m2)
(5)
μ0=4π×10−7 (Hm)
(6)
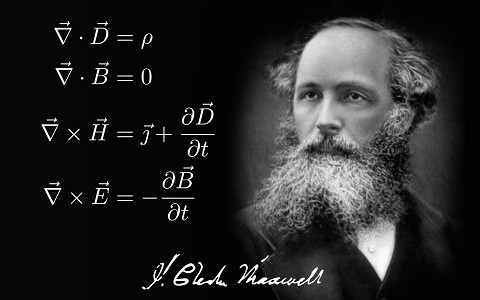
معادله موج
در ادامه از فرم دیفرانسیلی معادلات ماکسول به معادله موج خواهیم رسید. با گرفتن کرل از دو طرف قانون فارادی (معادله ۳)، روند محاسبه سرعت نور را آغاز میکنیم. با گرفتن کرل از رابطه (۳) داریم:
▽×(▽×E)=▽×–∂B∂t=–∂∂t(▽×B)
(7)
حال با استفاده از رابطه ریاضی زیر که به BAC-CAB معروف است، سمت چپ رابطه (7) را بازنویسی میکنیم.
▽×(▽×E)=▽(▽.E)–▽2E
(8)
در اینجا با توجه به رابطه (۱)، جمله ▽.E=0 صفر میشود. در نتیجه رابطه (۷) با استفاده از رابطه (4) برای سمت راست تساوی، به صورت زیر در میآید:
▽(▽.E)–▽2E=–μ0ε0∂2E∂t2
(9)
⇒▽2E=μ0ε0∂2E∂t2
(10)
اگر دقت کرده باشید، با انجام روند فوق، به معادله موج الکترومغناطیسی رسیدیم. به عبارت دیگر، رابطه (10) معادله موج مولفه میدان الکتریکی امواج الکترومغناطیسی را در ۳ بعد تشریح میکند. معادله موج مولفه مغناطیسی نیز به صورت مشابه با روند فوق، با گرفتن کرل از دو سمت معادله قانون آمپر – ماکسول (رابطه ۴) به فرم زیر به دست میآید.
▽2H=εμ∂2H∂t2
(11)
جهت سادگی کار فرض میکنیم که موج یک بعدی است. در نتیجه رابطه (10) به صورت زیر نتیجه میشود:
∂2E∂x2=μ0ε0∂2E∂t2
(12)
جواب عمومی معادله دیفرانسیل فوق، به صورت زیر است:
f(k(x–vt))+g(k(x–vt))
(13)
که در رابطه فوق، متناسب با فیزیک مسئله، v سرعت و λ طول موج است. دو تابع f و g نیز جهت حرکت موج به سمت مثبت یا منفی محور را توصیف میکنند.
پاسخ معادله موج
از آنجایی که پاسخ فوق، عمومی است، میتوانیم رایجترین فرم، یعنی موج سینوسی را که در جهت مثبت حرکت میکند، انتخاب کنیم. در نتیجه:
E=E0sin[2πλ(x–vt)]
(14)
پارامتر E0، دامنه میدان الکتریکی است. حال دو سمت رابطه (12) را با گرفتن مشتق زمانی و مکانی از رابطه (14) به دست میآوریم.
∂2E∂x2=–E0(2πλ)2sin[2πλ(x–vt)]
(15)
∂2E∂t2=–E0(2πλ)2sin[2πvλ(x–vt)]
(16)
با جایگذاری روابط فوق در رابطه (12)، نتیجه میشود:
–E0(2πλ)2sin[2πλ(x–vt)]=–μ0ε0E0(2πvλ)2sin[2πλ(x–vt)]
(17)
⇒(2πλ)2=μ0ε0(2πvλ)2
(18)
⇒1=μ0ε0v2
(19)
حال با تنها کردن پارامتر سرعت v و جایگذاری مقادیر عددی ضریب گذردهی الکتریکی و مغناطیسی خلأ مقدار سرعت زیر به دست میآید:
⇒c≡v=1√μ0ε0≅299,792,458≅3×108 (ms)
(20)
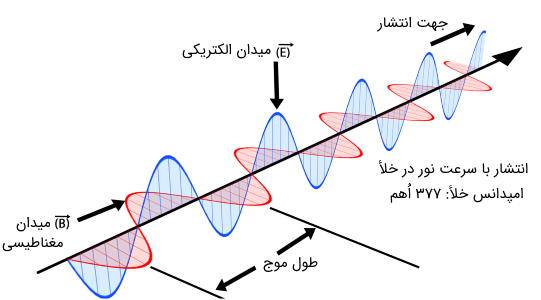
سرعت به دست آمده در بالا، نهایت سرعتی است که امواج الکترومغناطیسی یا فوتون وابسته به آنها میتواند داشته باشد. در فیزیک اغلب سرعت نور را با پارامتر c نمایش میدهند. رابطه (19) به صورت کلی زیر نیز بیان میشود. با توجه به رابطه زیر، سرعت به دست آمده کمتر از سرعت نور (3×108 (ms)) میشود.
v=1√με
(21)
ضریب شکست

دقت داشته باشید که سرعت نور یا امواج الکترومغناطیسی همواره مقدار ثابت به دست آمده در رابطه (20) نیست. بازهم تاکید میکنیم که مقدار عددی مذکور، تنها نهایت سرعت ممکن برای امواج الکترومغناطیسی است. به عبارت دیگر، اگر امواج الکترومغناطیسی در محیط خلأ منتشر شوند، سرعتشان برابر با مقدار (3×108 (ms)) است. اجازه دهید این مقدار را با پارامتر c نمایش دهیم.
سرعت امواج الکترومغناطیسی در سایر محیطهای مادی، همواره کمتر از مقدار c است. جهت سنجش و بررسی سرعت نور یا امواج الکترومغناطیسی در محیطهای مادی، پارامتری موسوم به ضریب شکست معرفی میشود. به بیانی ساده، ضریب شکست که آن را با نماد n نمایش میدهند، نسبت سرعت نور در خلأ (c) به سرعت نور در آن محیط (v) تعریف میشود. یعنی:
n=cv=3×108 (ms)v (ms)
(22)
بنابر تعریف فوق، ضریب شکست خلأ برابر با یک در نظر گرفته میشود. چرا که سرعت امواج الکترومغناطیسی در خلأ برابر با مقدار c=3×108 (ms) است. حال در نظر داریم تا با استفاده از رابطه فوق و رابطه سرعت موج (21)، رابطه دیگری را برای ضریب شکست به دست آوریم. از رابطه (22) نتیجه میشود:
v=cn
(23)
حال از رابطه فوق و (21)، میتوان نسبت سرعت موج در دو محیط با خواص الکترومغناطیسی مختلف را به شکل زیر نوشت:
v1v2=n2n1=√ε2μ2ε1μ1
(24)
در صورتی که دو محیط مغناطیسی نباشند، میتوان ضریب نفوذپذیری (تراوایی) مغناطیسی را برای هر دو آنها μ=μ0 در نظر گرفت. در نتیجه:
v1v2=n2n1=√ε2ε1
(25)
نتیجه جالب توجهی که میتوان از رابطه فوق گرفت، رسیدن به رابطهای جهت محاسبه ضریب شکست محیط است. در واقع اگر محیط n1 را خلأ فرض کنیم (n1=1)، ϵ1≡ϵ0 شده و در نتیجه:
n=√εε0
(26)
ضریب شکست بر حسب امپدانس محیط
در مقاله «دی الکتریک — به زبان ساده» دیدیم که پارامتر گذردهی الکتریکی ε را میتوانیم به شکل ε=ε0εr بنویسیم که در آن εr به ثابت دیالکتریک موسوم است. ثابت دیالکتریک خود با پذیرفتاری الکتریکی χe به صورت εr=1+χe رابطه دارد. در نتیجه ضریب شکست (عامل تعیین کننده سرعت نور در محیط) در یک محیط دی الکتریک به صورت زیر تعریف میشود.
n=√εε0=√ε0εrε0=√εr=√1+χe
(27)
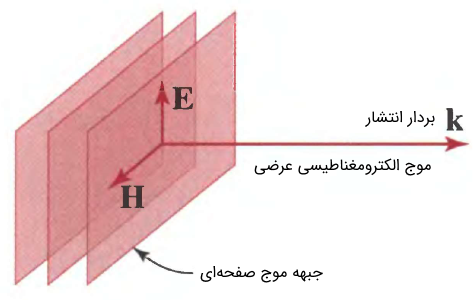
در مقاله «امپدانس ذاتی محیط — به زبان ساده» دیدیم که ضریب شکست را بر حسب امپدانس موج یا امپدانس محیط نیز میتوان بیان کرد. امپدانس موج η در حالت کلی، به صورت نسبت دامنه میدان الکتریکی E0 به دامنه میدان مغناطیسی H0 تعریف میشود؛ یعنی:
η=E0H0=cμ=√με
(28)
با توجه به تعریف ε=ε0εr و μ=μ0μr، نتیجه میشود:
η=E0H0=cμ=√με=√μ0μrε0εr=√μ0ε0√μrεr=η0√μrεr=377√μrεr
(29)
⇒η=η0√μr√εr=η0√μrn
(30)
در صورتی که محیط مغناطیسی نباشد، μr برابر با یک بوده و رابطه به صورت η=η0n ساده میشود.
